logisticsiop.blogg.se

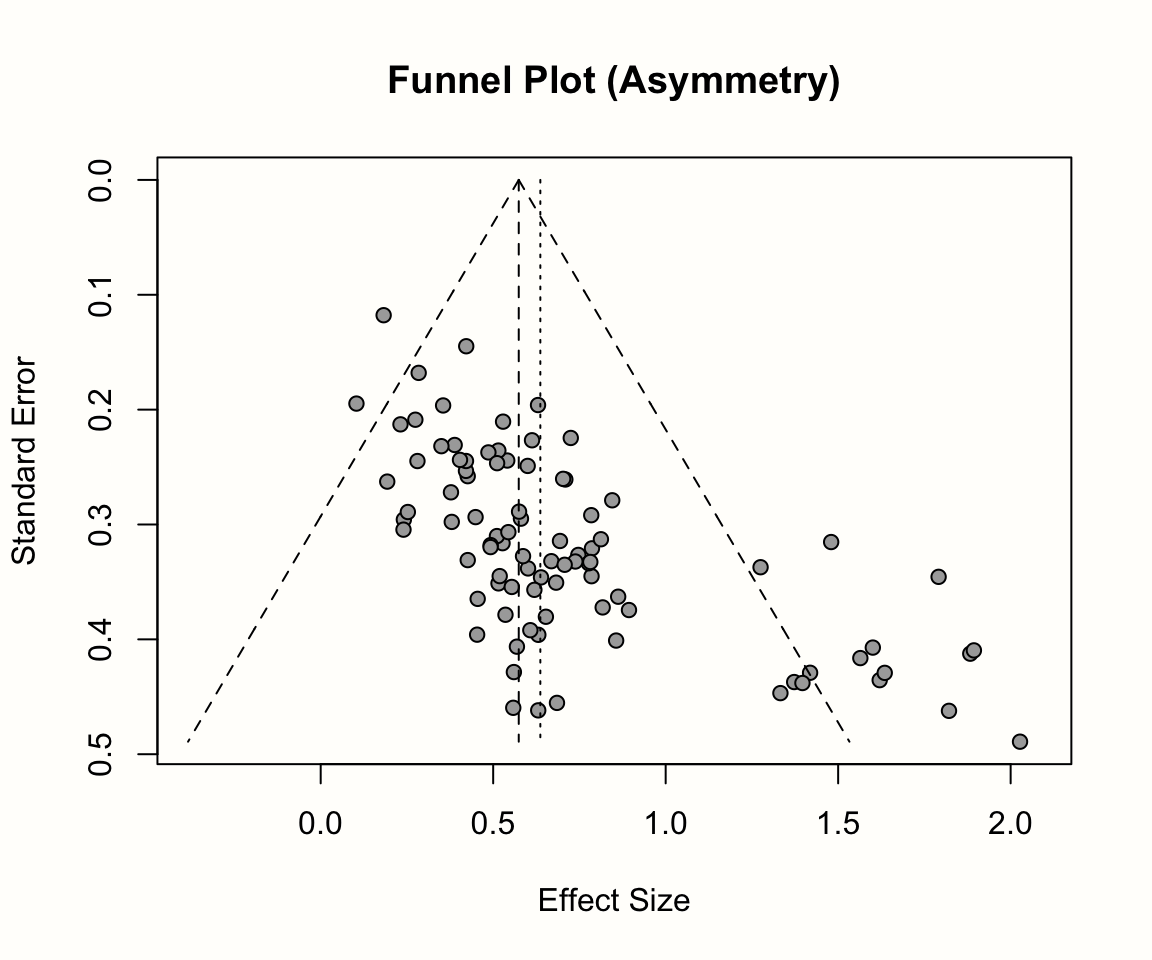
The most important difference is that diagnostic accuracy of a test is generally measured by a pair of summary points, namely, sensitivity and specificity. There are several unique characteristics of meta-analysis of diagnostic test accuracy studies compared to therapeutic/interventional studies ( 8, 10). These methods provide either summary points of different accuracy parameters (for example, sensitivity, specificity, positive and negative likelihood ratios, and diagnostic odds ratio for definitions, please refer to Part I of this two-part review) or a summary receiver operating characteristic (SROC) curve ( 9). Several different methods have been proposed for meta-analysis of diagnostic test accuracy studies ( 1, 2, 3, 4, 5, 6, 7), but there is still considerable uncertainty regarding the best method to synthesize those studies ( 8). Ideally, an analytic method used for this type of meta-analysis should estimate diagnostic accuracy with the least bias, incorporating various factors known to affect the results.

Meta-analysis of diagnostic test accuracy studies is a useful method to increase the level of validity by combining data from multiple studies. This article could serve as a methodological reference for those who perform systematic review and meta-analysis of diagnostic test accuracy studies. We provide a conceptual review of statistical methods currently used and recommended for meta-analysis of diagnostic test accuracy studies. Hierarchical models including the bivariate model and the hierarchical summary receiver operating characteristic model are increasingly being accepted as standard methods for meta-analysis of diagnostic test accuracy studies. Since sensitivity and specificity are generally inversely correlated and could be affected by a threshold effect, more sophisticated statistical methods are required for the meta-analysis of diagnostic test accuracy. Meta-analysis of diagnostic test accuracy studies differs from the usual meta-analysis of therapeutic/interventional studies in that, it is required to simultaneously analyze a pair of two outcome measures such as sensitivity and specificity, instead of a single outcome.